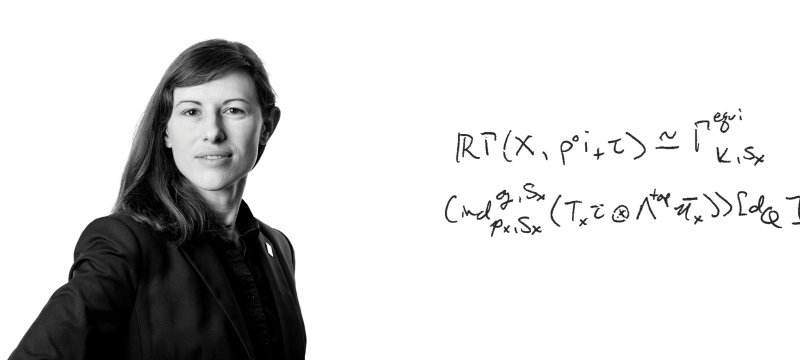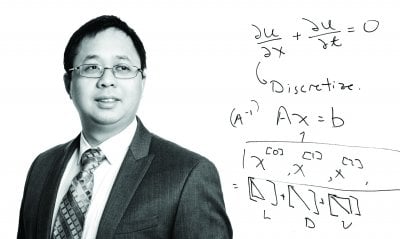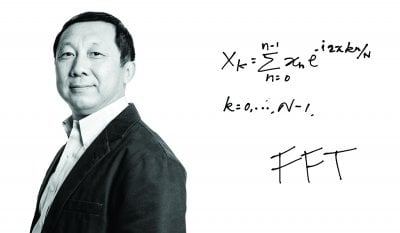STEM: science, technology, engineering, and of course, mathematics. It’s time for math to take centerstage.
When most people talk STEM, they’re likely focused on S-T-E. If math is at all mentioned, it’s a polite—perhaps intimidated—nod to the orchestra pit. Because math, as the popular attitude goes, should be left to the nightmares of seventh-grade algebra. Not surprising given that the National Institutes of Health report 93 percent of adults in the US experience some level of math anxiety.
There are those who enjoy a bit of numerical play. We expect them to become engineers (because, of course, engineers have to like math). But straight-up mathematicians? They’re a rare and different breed.
And to see research problems through their eyes is to know truth and beauty. Math is as much an art as it is a major influence on other STEM fields. Particularly with applied math, where models and algorithms provide foundational support in scientific and technological endeavors, the M of STEM joins the chorus or keeps behind the curtains to work the grand sets of modern research. The show could not go on without mathematics.
So in these pages, applied math sings its own aria.
Overture Upon Detonation
A surprising problem in the field of partial differential equations is that of instantaneous detonation.
Take a two-meter-long tube, for example. If an explosion sets off in one end, how quickly does it travel through the rest of the tube? In true Hollywood style, the blast would be nearly instantaneous—and with just enough time, the main character jumps away. But the problem is that if we zoom in on the explosion, slowed the scene way down, and tried to measure the fiery movement tick-tick-tick down the tube, we wouldn’t be able to come up with a precise mathematical model that perfectly replicates what we observe in real life.
This bothers mathematicians. “Math always tells you the truth,” says Yang Yang, an associate professor of applied mathematics, explaining one solution to the instantaneous detonation problem is to add more ticks in the measurement, which creates its own challenge. “With more variables, you need more equations.”
Enter one of the most common misconceptions about mathematics: Math is entirely about numbers. That’s like saying singing is about the notes. So, throwing in more numbers or more variables to a mathematical model is not always ideal, although greater computing power with facilities like the Michigan Tech high-performance computing facility Superior and advances in math theory have certainly expanded research horizons with more data and complexity. However, what applied mathematicians like Yang are truly interested in is how to streamline and verify models.
“Engineers use mathematical models to solve concrete problems—math is a tool,” Yang says, clarifying that in his world, math is a mindset. “Applied mathematicians need to understand those engineering problems and ensure the math is consistent. The solution you find should follow common sense.”
"I work with equations that describe the world around us."
Yang, who contributes to research in chemical engineering and cosmology, says models are less about numbers and more about relationships. Whether he is developing models for the shift of stars or the movement of oil in a rock formation or compressible flow in gas dynamics, he seeks to preserve the observable physical properties of variables while upholding the truth of the mathematical relationships. There is no “close enough” in this perspective. When a blast goes off in one end of a tube and we try to predict the movement, the model is either right or wrong. Since it’s still wrong, there are seemingly infinite opportunities to improve, and plenty of job security in applied mathematics.
The Ballet in Parallel
Another misconception about math: Show your work; a single right answer means a single methodology. Models may be right or wrong—but there’s no silver bullet. Many mathematicians tackle similar problems with many different approaches.
Cécile Piret, associate professor of applied math, contributes to research in physics and geology and reworked the infamous Calc 3 coursework. It is a tension in the difference between what is observed in experiments and what a model predicts that drives the field, she says: “Why does the simulation not represent what happens in nature? Either the mathematical representation of the phenomenon is wrong, or it is correct in which case the computational method used is inaccurate. Part of my job is to ensure that the method used is as accurate as possible.”
Accuracy is not the only demand; efficient and computationally inexpensive methods are also prized. Geologists, physicists, and other scientists are not mathematicians, and some of their analytical tools do not meet the rigorous standards of applied math, which presents opportunities that applied mathematicians happily delve into. When given enough time, these collaborations drive innovation and foster new techniques.
Piret works with a relatively new mathematical tool called radial basis functions method, or the stoic acronym RBF. The method can describe complex geometries with exquisite accuracy—the curve of a rock formation, the plane of an aquifer, the slippery slope of a muddy hill about to give way. Instead of relying on meshes and grids, the RBF method just requires a set of points that naturally follows the complexities of the domain.”
Another way to look at changes over time is to sketch it out first. Benjamin Ong, assistant professor of computational mathematics, tackles mathematical problems in computing. Sketching data is a method that Ong and his students study by looking at the underlying structures in a dataset that could help speed up computation. For example, if you know the data is linear, then it’s easier to predict the slope and direction of the line rather than wasting time determining that it’s not a logarithmic regression or parabola. In another project, Ong works on a family of methods called parallel-in-time; the idea, relatively new in the US, is to generate a solution quickly to ensure that the simulation is on track. Using the parallel-in-time method, the model makes a prediction then simultaneously assesses it while making another. In parallel steps, the model predicts and assesses, constantly improving its outputs as it goes.”
“It’s problem agnostic,” Ong says. “Applied mathematics is about versatility.”
Underground and See-Through, a Finale
Versatility takes applied mathematics into unexpected spaces—like deep in a subterranean labyrinth with a fleet of drones or through walls.
“If someone is standing on the other side of a wall, how do you know?” asks Jiguang Sun, professor of applied math, who often works with geophysicist collaborators interested in developing ways to see deep into the earth using electromagnetic waves; the challenge is figuring out what is what based on the wave signatures. “How can you tell the difference? What are the reflection patterns?”
Sun and his team were able to develop pattern recognition for ultrawideband radar tech using an algorithm called a fast Fourier transform. As Sun puts it, it all comes down to wave equations and those equations are treated all the same in math, so finding differences in the equations means pulling in enough data to separate the signal from the noise. “Big Data does not simply mean lots of data,” he says. “It’s about extracting useful information.”
In the case of pulling a fast Fourier on through-wall detection, the solution came down to predictable periodic movement—a person’s breath. Inhaling and exhaling created enough stir in the wave equations to reveal a person on the other side of the wall.”
"Math does not belong to science, technology, and engineering. It is a different perspective, a precise way to understand, explain, and view the world."
In essence, this is what all research is about: Starting with a question and following a clear logic to seek an answer. This deceptively simple idea is one of the reasons math is so ubiquitous in the other STEM fields. And in practice the math and the applications only get more complex.”
“You learn to abstract away the complexity to get to the crux of a difficult problem,” says Sarah Kitchen, a research scientist with the Michigan Tech Research Institute (MTRI), who leads a project called Bayesian Adaptive Robot Control System (or BARCS, a good Husky name). BARCS placed second in the virtual track during the latest round of Defense Advanced Research Projects Agency's (DARPA) Subterranean Challenge last October. The demanding environment, a partially collapsed mine with many obstacles being explored by a fleet of drones, looks like a video game. Successfully navigating it draws on Kitchen’s background in representation theory, and while she doesn’t use this form of pure math directly, it drives her thinking on challenging system-scale problems. Working with robotics engineers and software developers now, Kitchen takes tools from different math fields and finds new applications, using a mathematical eye to cut through complex strings of equations and algorithms to get at the heart of the system’s components and how they relate.”
Kitchen’s MTRI colleagues, including Susan Janiszewski, Mark Stuff, Ismael Xique, and Joseph Lindgren, Meryl Spencer, Sean Kelly, and Erick Vega, also draw on their math backgrounds to solve difficult engineering and ecological problems. Janiszewski loves the challenge of figuring out how to apply mathematical frameworks to real-world conundrums.
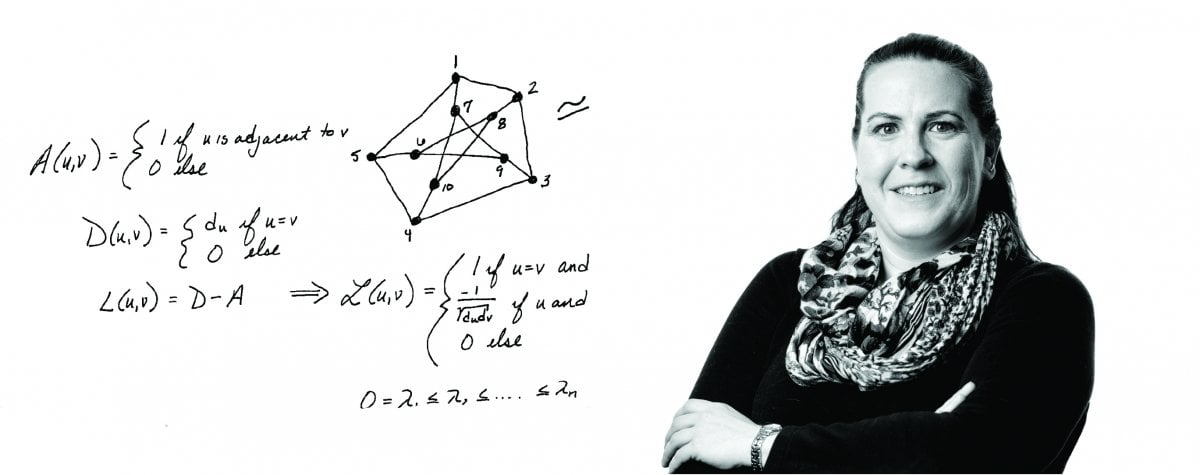
“When people think of graphs, it’s visual,” Janiszewski says, bringing up another misconception about mathematics: Math can always be visualized. “But it’s really about relationships and once those relationships are on a graph we can use graph theory. When you get into graphical representation, then all of linear algebra is at your disposal.”
To put it back into the broader context: Math is not static. Math is not just about the numbers, solving for the right answer, or how it plots on a graph. Math is more versatile and dynamic than any non-mathematician could imagine, which is why we all keep coming back to them with our STEM challenges. But rather than seeking them out for mere number-crunching, we can take a moment with the final note hanging in the air to appreciate the artistry that is the mindset and practice of applied mathematics.
Michigan Technological University is an R1 public research university founded in 1885 in Houghton, and is home to nearly 7,500 students from more than 60 countries around the world. Consistently ranked among the best universities in the country for return on investment, Michigan's flagship technological university offers more than 185 undergraduate and graduate degree programs in science and technology, engineering, computing, forestry, business, health professions, humanities, mathematics, social sciences, and the arts. The rural campus is situated just miles from Lake Superior in Michigan's Upper Peninsula, offering year-round opportunities for outdoor adventure.