There’s a method to my partial differential equations.
Yang Yang, associate professor of mathematical sciences, uses high-order numerical techniques to solve mathematical models with unbounded singularities — points in models that defy predictions of what might occur at those points.
Because Yang’s work in pure mathematics is so deeply theoretical, it can be difficult for those outside the field to understand what he does. In the following, we’ve embraced a tactic of heavily mixed metaphors to explain a facet of Yang’s science.
Think for a moment about a basketball: If you squeeze it as hard as you can until the volume becomes smaller, the density of the smaller ball will be greater than the ball at its original size. If we put the basketball in a vice and squeezed the ball until the volume approaches zero, the density could be infinite — an unbounded singularity.
It’s worth noting that singularities are imaginary constructs; they’re a kind of mental placeholder for unpredictability in modeling. In Yang’s case, the singularities are the density of a point approaching zero volume.
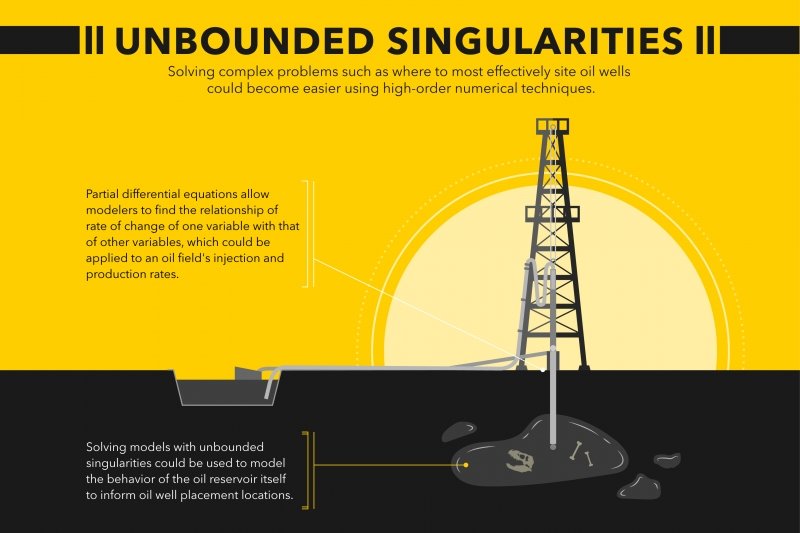
However, singularities make it difficult to model complicated situations. The ability to anticipate when singularities happen has the potential to greatly improve computer modeling in a variety of fields, ranging widely from astrophysics to biology. Moreover, accurate approximations of singularities can also improve the simulation results in oil recovery and electrical engineering.
As an example, in an oil field, every time an extraction company digs a well, it costs a great deal of money. If those companies are able to model the behavior of the oil reservoir itself to inform oil well placement locations as well as the injection and production rate, the model can save the company a lot of time and exploratory drilling efforts.
Continuing to mix metaphors, unbounded singularities could be compared to playing a game of Battleship, except the size of the gameboard is unlimited. Pinpointing the opponent’s ship positions (singularities) and the trajectories of the ships are what Yang’s methods do. Yang uses partial differential equations because they find the relationship of one variable’s rate of change with that of other variables.
Specifically, Yang uses high-order numerical methods: Using polynomials to approximate unknown functions. Polynomial functions are continuous and smooth — bell curves or curves that show exponential increases or decreases.
“Consider the polynomial as the basketball, we squeeze it and keep the total mass,” Yang said. “When the volume is small, it can be considered as an approximation of the singularity.”
However, such an approximation may not preserve some physical features, and suitable numerical techniques have to be applied. To do that, Yang replaces the unknown function with polynomials to construct several equations, then uses a Fortran and MatLab to find out the polynomials.
Michigan Technological University is an R1 public research university founded in 1885 in Houghton, and is home to nearly 7,500 students from more than 60 countries around the world. Consistently ranked among the best universities in the country for return on investment, Michigan's flagship technological university offers more than 185 undergraduate and graduate degree programs in science and technology, engineering, computing, forestry, business, health professions, humanities, mathematics, social sciences, and the arts. The rural campus is situated just miles from Lake Superior in Michigan's Upper Peninsula, offering year-round opportunities for outdoor adventure.





Comments